We are studying many biological phenomena using theoretical methods, including mathematical and computational analyses. Theoretical methods are useful to decipher large amount of information, and to give an integrative understanding for the complex biological systems.
-
Complete control of a gene regulatory network of ascidian embryo by a few factors identified by a mathematical theory.
Present WorksIt is believed that dynamics of regulatory networks between bio-molecules are the origin of biological functions. We have developed Linkage Logic theory, by which key molecules for the dynamics of a whole system are determined from information of regulatory linkages alone. Using the theory, we analyzed a gene regulatory network for cell-fate specification system, and could control the system successfully.
VIEW MORE -
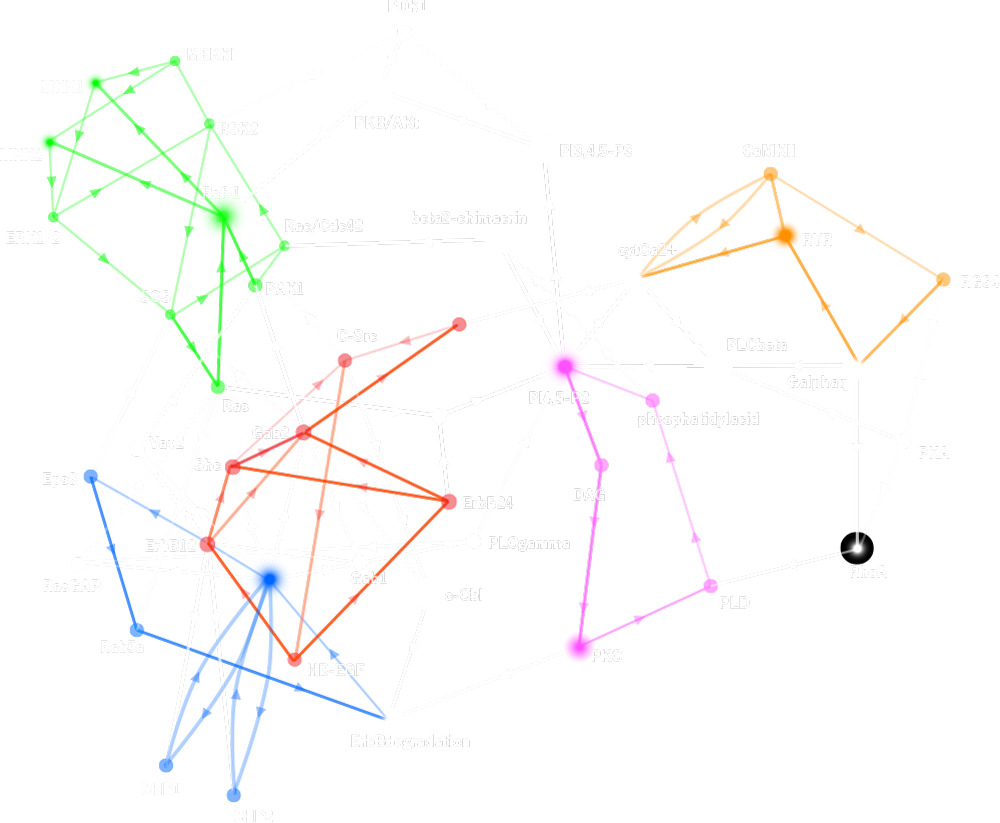
Determining responses of chemical reaction systems from structure of networks
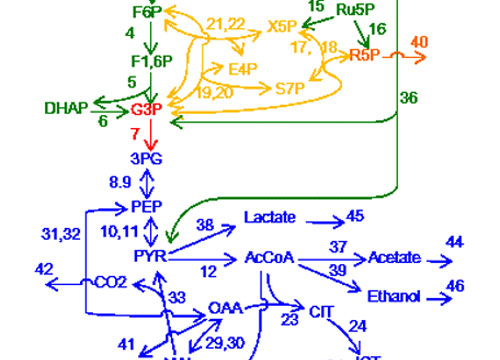
Present WorksThe biological functions of a cell arise from a large set of chemical reactions, which are connected by sharing their products and substrates and constructing a large network. We develop a mathematical method, by which responses of chemical reaction networks towards perturbations of any enzymes in the system from structure of network alone. We found a general law which directly connects the network topology and responses, and governs the response patterns of reaction systems.
VIEW MORE -
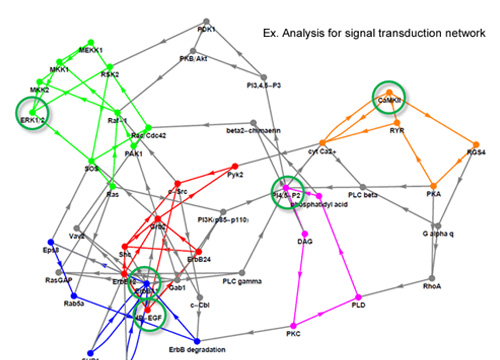
Structure and dynamics of regulatory networks
Present WorksModern biology provides many networks describing regulations between many species of molecules. It is widely believed that the dynamics of molecular activities based on such regulatory networks are the origin of biological functions. In this study we develop a new theory to provide an important aspect of dynamics from information of regulatory linkages alone.
VIEW MORE -

Physics of organelle morphogenesis
Present WorksOrganelles in a cell show wide variety of morphogenesis of membrane stricture, which are specific to the types of organelles. Considerable ratio of the diversity of morphogenesis can be understood by our mathematical model based on statistical physics.
VIEW MORE -

Understanding cell movements from image analysis
Present WorksIn order to understand emergence of biological functions in development, we have to understand the dynamics of cell population including cell movements, cell division and cell death. We study the dynamics of cell population by combining image analysis from experimentally obtained pictures and mathematical modeling to estimate the regulation among cells.
VIEW MORE -
Auxin pattern formation in plant development
Present WorksMorphogenesis of plants in development is considered to be governed by pattern formation of auxin distribution, which is mediated by polarization of PIN in membrane of cells. However, we do not yet understand fundamental mechanisms for generating biologically functions from the spontaneous pattern formation of auxin.
VIEW MORE Pattern formation in heterocyst differentiation in multicellular cyanobacteria
Present WorksThe multicellular cyanobacteria show differentiation of special type of cells, heterocyst, under nitrogen-deprived condition, which appear in regular manner with distance of about 10 cells. We studied the mechanism of regular pattern formation of heterocyst by combining experimental observations and mathematical modeling.

Mathematical models for pattern formation of dendrites of neurons
Present WorksDendrite is a neuronal process which is specialized for receiving and processing synaptic or sensory input. A remarkable feature of dendrite is its morphological diversity. The shapes of dendritic trees are characteristic of individual neuronal types and they are highly variable from one neuronal type to another.
VIEW MORE