- HOME
- Research
- Present Works
- Mathematical models for pattern formation of dendrites of neurons
Present Works
Mathematical models for pattern formation of dendrites of neurons
Dendrite is a neuronal process which is specialized for receiving and processing synaptic or sensory input. A remarkable feature of dendrite is its morphological diversity. The shapes of dendritic trees are characteristic of individual neuronal types and they are highly variable from one neuronal type to another. This diversity contributes to differential processing of information in each type of neuron. Therefore, patterning neuronal class-specific dendrites is a process to produce forms that realize physiological functions of neurons. However, a comprehensive logic of dendrite development has not been formulated yet.
We developed a new class of dendrite growth model, which represents all extension, orientation of growth and branching of dendrites in a single scheme. In addition, this model has explicitly incorporated an underlying biological mechanism, that is, competitive interactions between neighboring dendrites
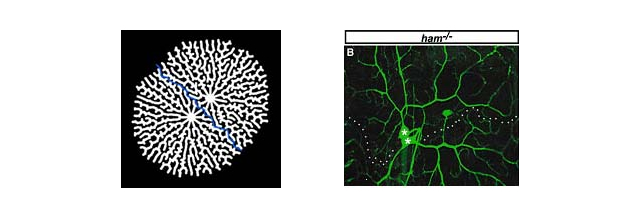
A key point in our modeling is to couple chemical dynamics to dendrite growth. In our model, we distinguish two spatial compartments: inside and outside regions of neurons. The cell compartment dynamically grows under the regulation of a chemical reactant activator. Thus we call our model a “cell compartment model”. The activator reacts with another reactant suppressor in the way of the reaction-diffusion (RD) model of the so-called “Activator-Inhibitor type” (Turing, 1952; Gierer and Meinhardt, 1972). We set a restriction in the 2D space so that the activator only diffuses inside of the cells. These settings endow the system with feedback loop regulations at two different levels: one between two chemicals, and another between the dynamics of the chemicals and the expansion of the cell compartment. Using this formula, we study the dynamics of dendritic branch formation. Computer simulation showed that the cell compartment model developed dendritic branching autonomously and numerical analysis determined the conditions that allow it.
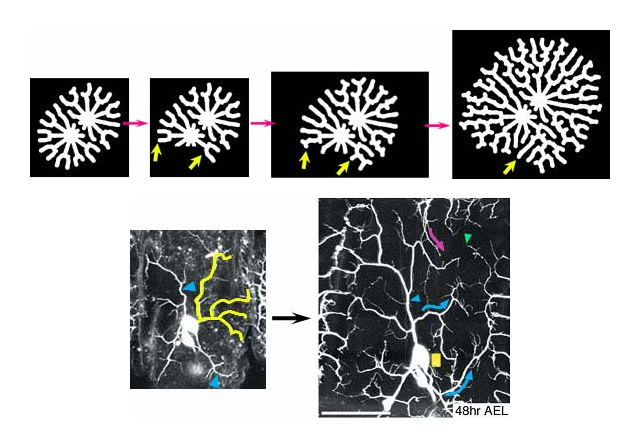
This work is collabolation with Dr.T.Uemra and Dr.K.Sugimura in Kyoto University (Sugimura K., Shimono K., Uemura T. and Mochizuki A (2007) Self-organizing mechanism for development of space-filling neuronal dendrites. PLoS Comput Biol. 3(11), 2143-2154.).