- HOME
- Research
- Past Works
- A theoretical study for gene regulatory networks and analysis of differentiated cell-states
Past Works
A theoretical study for gene regulatory networks and analysis of differentiated cell-states
The highly complex behavior of organisms is based on the interactive regulation of genes, functioning together to create a gene network. The regulation of gene expression levels is dependent on the concentrations of transcriptional regulators.Typically, multiple transcription factors can bind to the regulatory region of a gene; each factor may independently affect the gene expression levels. In this manner, the regulatory region of gene serves as an integration point, performing a logical computation of these transcription factors to determine the resulting gene expression levels. In addition, once translated, the encoded protein may control the transcription of other genes.
The complexity of gene networks has been considered to be a problem that may be solved from a theoretical point of view. Since the proposal of the Boolean model by Kauffman, multiple mathematical models have been invented and analyzed to study complex gene networks. There are two general classes of network models, discrete and continuous models.Continuous models are likely more realistic than discrete models as a representation of biological systems. However, the dynamical behavior of continuous models is analyzed much less than that of discrete models.
I have developed a model for gene networks in a framework of continuous time and state variables. I analyze steady states appearing in this system in general way. The steady states specify distinct cell states defined by patterns of gene activity. I introduce three types of steady states observed in a continuous time and space model, whose values and stability can be evaluated from the structure of gene regulatory interactions. The expected numbers of steady states in a randomly generated gene network were derived in exact forms. I determined the distribution of the steady states in a randomly generated network.
The results were surprising; the number of steady states in a random gene network does not depend on gene number. In addition, the number of steady states is very small; the number of RSPs, in which the activity of each gene is either on or off, is only one. Most randomly generated gene networks will have only a few (or no) steady states, despite the presence of many genes in the system. Thus, increases in the number of genes do not augment the number of steady states for gene activity. The gene expression steady states may correspond to differentiated cell type identities. Thus, this result implicates that the number of genes is not the driving force increasing the diversity of differentiated cell types or the complexity of organisms.
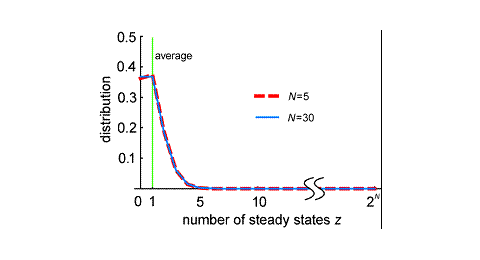
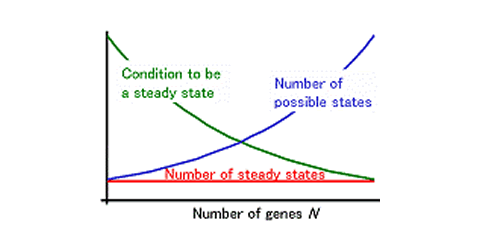
In reality, multi-cellular organisms have a wide variety of differentiated cells. Why, then, do the networks in actual organisms have multiple steady states? It seems likely that the networks within actual organisms are quite biased from the average randomly generated network. A gene network including a large number of self-regulatory genes has a large number of steady states. Thus, self-regulation within a gene network may be the main source of cell type diversity in actual organisms (Mochizuki, A. (2005) An Analytical Study of The Number of Steady States in Gene Regulatory Networks. J. theor. Biol. 236, 291-310.).